티스토리 뷰

👉 자주 쓰이는 데이터 형
| 숫자 | 정수(int) | -30, -46656, 0, 23, 333 ... |
| 실수(float) | -0.3737, -376.0, 0, 3.14, 256.333 ... | |
| 복소수(complex) | 실수와 허수의 합의 꼴로써 나타내는 수 | |
| 문자열(string) | 'a', 'b', 'abc', 'apple', 'I am happy!', “안녕하세요” | |
| 불(boolean) | True, False | |
| 리스트 | ['홍길동', 32, '010-2222-3333', 'hong@korea.com'] | |
| 튜플 | ('짜장면', '짬뽕', '탕수육', '우동') | |
| 딕셔너리 | {'red':'빨간색', 'yellow':'노란색', 'blue':'파란색', 'green':'초록색'} | |
👉 정수형 (Integer)
n1, n2, n3, n4, n5 = 33, -44, 0, 7, 88, 38784✔ 정수는 음수, 0, 양수로 구성된 숫자를 말한다. (파이썬에서는 unsigned를 제공하지 않는다)
✔ 데이터 타입마다 크기가 정해져 있는 다른 프로그래밍 언어와 다르게, 파이썬에서는 정수에 크기가 정해져 있지 않다.
✔ 그렇기 때문에 메모리가 허용하는 한 무한대의 정수를 다룰 수 있다. 이는 속도가 떨어지는 원인이기도 하다.
online = 0
offline = 1✔ 프로그래밍에서 정수는 정보를 압축해 사용하기도 한다.
✔ 예를 들어 온라인 상태라면 0, 오프라인이라면 1로 표현할 수 있다.
✔ 이런 경우 크기가 정해지지 않은 정수를 사용한다면, 메모리 낭비가 클 수밖에 없다.
+12 0000 0000 0000 1100✔ 10진수로 표현된 정수 12를 2진수로 표현하면 1100이다.
✔ 그렇다면 -12를 2진수로 표현하려면 어떻게 해주어야 할까?
+12 0000 0000 0000 1100
-12 1000 0000 0000 1100 (+)
1000 0000 0001 1000✔ 가장 첫 번째 비트는 부호 비트이다. 양수라면 0, 음수라면 1로 표현한다.
✔ 첫번재 비트를 음수를 의미하는 1로 바꾸어 주었다. 이렇게 되면 -12인지 확인해보자.
✔ 같은 절댓값을 가지고 부호가 다른 값을 서로 더해주면 0이 되어야 한다. (예) 12 + (-12) = 0
✔ 부호 비트를 바꾸어 준다 해도 이는 음수가 아님을 알 수 있다.
+12 0000 0000 0000 1100 #1의 보수 구하기
1111 1111 1111 0011 #1 더하기
1111 1111 1111 0100 #절대값이 같은 음수
+12 0000 0000 0000 1100
-12 1111 1111 1111 0100 (+)
0000 0000 0000 0000✔ 음수로 2진수를 표현하기 위해서는 먼저 같은 절댓값을 가지는 양수의 1의 보수를 구해야 한다.
✔ 그다음 1의 보수에 +1 해주어 2의 보수를 구하면 된다.
✔ 그리고 두 수를 더해보면 0이 나오는 것을 확인할 수 있다.
r 진법 수 : ( r - 1 )의 보수 + 1 = r의 보수
✔ 합이 0 이 된다는 것은 결국 자릿수가 하나 증가하여 0 이 된다는 것을 의미한다.
✔ 즉, 10진수의 경우 한자리 수에서 두 자릿수로 넘어가는 10의 보수를, 2진수의 경우는 2의 보수를 구하면 된다.
✔ 만약 이를 구하기 어려운 경우 먼저 -1 한 보수를 구하고(10진수는 9의 보수, 2진수는 1의 보수)
✔ 1을 더해주면 좀 더 쉬운 연산이 가능하다. 공식처럼 기억해두자.
(예) 8의 10의 보수 = 2 / 8의 9의 보수 = 1 → +1 하면 10의 보수 값과 같다.
16진수 접두사 : 0x
2진수 접두사 : 0b
8진수 접두사 : 0o✔ 정수는 일반적으로 10진수로 표현하지만 2진수, 8진수, 16진수로도 표현할 수 있다.
✔ 기본적으로 2진법, 8진법, 16진법은 양태 표현만이 가능하므로, 음수가 존재하지 않는다.
✔ 진법을 바꾸는 아래 함수들은 오차가 발생할 수 있으니 사용하지 않는 것을 권장한다.
#10진수를 2진수로 변환
print(bin(0)) #0b0
print(bin(8)) #0b1000
print(bin(32)) #0b100000
print(bin(255)) #0b11111111
#2진수를 변수에 할당
a = 0b100
print(a) #4✔ bin()함수를 사용해서 10진수를 2진수로 변환할 수 있다.
#10진수를 8진수로 변환
print(oct(8)) #0o10
print(oct(10)) #0o12
print(oct(64)) #0o100
#8진수를 변수에 할당
a = 0o10
print(a) #8✔ oct()함수를 사용해서 10진수를 8진수로 변환할 수 있다.
#10진수를 16진수로 변환
print(hex(0)) #0x0
print(hex(255)) #0xff
print(hex(12345)) #0x3039
#16진수를 변수에 할당
a = 0xff
print(a) #255✔ hex()함수를 사용해서 10진수를 16진수로 변환할 수 있다.
👉 실수형 (Floating Point, 부동 소수점)
f1, f2, f3, f4, f5 = 3.14, -38.33, 0.0, 4567.785, 23.1✔ 간단하게 말하면 소수점이 있는 숫자를 의미한다.
✔ 파이썬에서는 실수를 부동 소수점 방식으로 표현한다. 이는 소수점을 움직여서 소수를 표현하는 방식이다.
print(0.1+.0.2) #0.30000000000000004
print(0.1 + 0.2 == 0.3) #False
✔ 파이썬에서 0.1과 0.2의 합을 출력하면 0.3이 아닌 값이 나온다.
✔ 파이썬은 실수를 부동 소수점 방식으로 표현하는데, 부동 소수점은 실수 표현 시 오차가 발생한다.
✔ 그렇기 때문에 0.1 + 0.2 == 0.3의 논리식은 False를 반환한다.

✔ 파이썬에서 실수를 표현하는 방법에 대해 자세히 알아보자.
✔ 첫 번째 부호 비트는 실수가 양수인지 음수인지를 표현한다. 양수라면 0, 음수라면 1로 표현된다.
✔ 그리고 지수부는 11비트로 최대 2^2023으로 큰 값을 표현할 수 있다. (❔ 왜 2^2023이지 ❔)
#3비트 사용 #4비트 사용
000 = 0 0000 = 0
001 = 1 ...
010 = 2 1001 = 9
100 = 4 1010 = A(10)
101 = 5 ...
111 = 7 1111 = F(15)
# 8,9 표현X # B~F는 필요X✔ 0~9를 사용하는 10진법 숫자를 2진수로 표현하기 위해서는 3비트는 부족하고, 4비트는 남는다.
✔ 즉, 10진법 숫자를 표현하기 위해 3-4비트가 필요하다는 것을 알 수 있다.
✔ 가수부는 10진법을 표현해야 하므로 52//3=17, 52//4=13의 연산을 통해
✔ 대략 13~17개, 약 15개의 정수를 표현할 수 있음을 알 수 있다. (변환 체계마다 다르지만 일반적으로 그렇다)
✔ 그렇기 때문에 실수형을 지수 형태로 표현하지 않으면 메모리 한계에 부딪혀 오차가 발생한다.
✔ 오차의 발생은 오류가 아니므로, 오차가 쌓이고 쌓여서 결국 엉뚱한 값으로 돌아온다.
x = 12340000000000000.0 #가수부의 범위를 벗어나 오차 발생
x = 0.1234 * 10^17 #지수형태로 저장하면 가수부 범위 내✔ x를 있는 그대로 저장하면 실수의 가수부 표현 범위를 벗어나기 때문에 가수부에서 문제가 발생한다. (오차 발생)
✔ 그렇기 때문에 지수 표현법을 사용해 오차를 줄여주도록 하자.
from decimal import Decimal
print(Decimal('0.1') + Decimal('0.2')) #0.3✔ decimal 모듈의 Decimal 함수를 사용해 오차가 없는 고정 소수점으로 사용할 수 있다. (모듈 import 필수)
✔ 고정 소수점을 사용하면 숫자를 10진수로 처리해 정확한 소수점 자릿수를 표현한다고 한다.
from fractions import Fraction
print(Fraction('10/3')) #10/3
print(Fraction(10, 3)) #10/3✔ 순환 소수라면(3.333333...) 고정 소수점을 표현하는 Decimal 함수도 정확하게 표현할 수 없다.
✔ 이 경우는 fractions 모듈의 Fraction함수를 사용해 분수로 표현할 수 있다. (모듈 import 필수)
✔ 인수를 하나 사용한다면 작은따옴표로 분수를 감싸 넣어주고, 두 개의 인수를 사용할 때에는 콤마로 구분한다.
👉 문자열 (String)
str1, str2, str3, str4, str5 = 'a', 'abc', '가나다', 'hello wolrd!', '010-1234-5678'✔ 하나 또는 여러 문자로 구성된다. 문자열은 단 따옴표나 큰따옴표로 감싼다.
✔ 다른 형태의 데이터 타입이어도 따옴표로 감싸면 문자열로 인지한다.
✔ 다른 프로그래밍 언어와 달리 char형은 존재하지 않으며, 항상 문자열 즉 문자의 배열 형태로 저장된다.
str1 = 'ab'
print(str1) #ab
print(str1[0]) #a
print(str1[1]) #b
str2 = 'a'
print(str2) #a
print(str2[0]) #a✔ 문자열은 항상 문자의 배열 형태이므로, 문자열 변수명은 곧 주소 값을 의미한다
✔ 문자열 변수명에 첨자를 사용하면 문자 하나하나에 접근할 수 있다.
✔ 문자를 하나 저장하더라도 문자열로 저장됨을 확인할 수 있다.
#배열명[start:end:step]
x = 'Hello Wolrd!'
print(x) #Hello Wolrd!
print(x[0]) #H
print(x[0:3]) #Hel
print(x[5:]) # World!
print(x[-1]) #!
print(x[-3:]) #rd!
print(x[-4:-2] #lr
print(x[0:5:2]) #Hlo
✔ 파이썬에서 배열의 인덱스는 다양한 방법으로 사용할 수 있다.
✔ 대괄호 내부에는 최대 3개의 값을 넣을 수 있다.
✔ 순서대로 index의 start 지점, end 지점 (기준은 미포함), step의 단위를 의미한다.
✔ step의 경우 생략되면 1로 증가 단위가 설정된다.
✔ 마지막 출력문은 0~4번째 문자를 index를 2 증가하면서 출력한다. 즉 index 0,2,4에 해당하는 Hlo를 출력한다.
✔ end 값을 미포함하는 이유는 index는 0부터 시작하기 때문이다.
👉 불 (Boolean)
if 1 : print('true') #true
if 2 : print('true') #true
if not 0 : print('false') #false ✔ Boolean 은 True(1)와 False(0) 두 가지 값을 가진다
✔ True는 일반적으로 1로 표현되지만, 0이 아닌 모든 값을 True로 인지한다.
✔ 마지막 if문의 조건은 not연산을 사용해서 false를 true로 바꾸어주어 출력문이 실행되도록 했다.
👉 형변환(Casting)
a = 1
b = '123'
i = int(b) #'123'을 int로 형변환 → 123
f = float(a) #1을 float로 형변환 → 1.0
s = str(a) #1을 string으로 형변환 → '1'
b = bool(a) #1을 booleand로 형변환 → True
print(i,f,s,b,sep='/')
print(type(i))
print(type(f))
print(type(s))
print(type(b))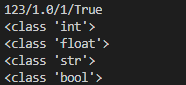
✔ 변경하고 싶은 데이터 형()을 통해 형 변환할 수 있다
str = '3.14'
#a = int(str) #에러 발생
a = float(str)
a = int(a)
print(a)✔ 문자열 변수에 실수 형태의 문자열이 저장되어 있다면, 바로 정수형으로 형변환할 수 없다.
👉 변수명이 의미하는 것
✔ 변수는 일반적으로 데이터를 담는 메모리 공간을 뜻한다.
✔ 하지만 파이썬에서는 데이터를 변수에 저장하는 것이 아니라 데이터, 즉 객체의 주소를 변수에 저장한다.
✔ 객체에 대한 주소 값을 변수가 가지고, 파이썬에서는 이를 레퍼런스로 취급한다.
✔ 파이썬의 레퍼런스 : C/C++의 포인터, 레퍼런스 개념이 혼재되었다. 물리적으로는 포인터지만 레퍼런스로 사용한다.
✔ 포인터로서의 특징 : 자체 저장 공간이 있어서 변경 가능 (대입 연산 가능)
✔ 레퍼런스로서의 특징 : 이름 자체가 객체를 의미 ( 포인터 연산 불가능(예) *(p+1), *(p+2) )
test = {10,"test", 20}
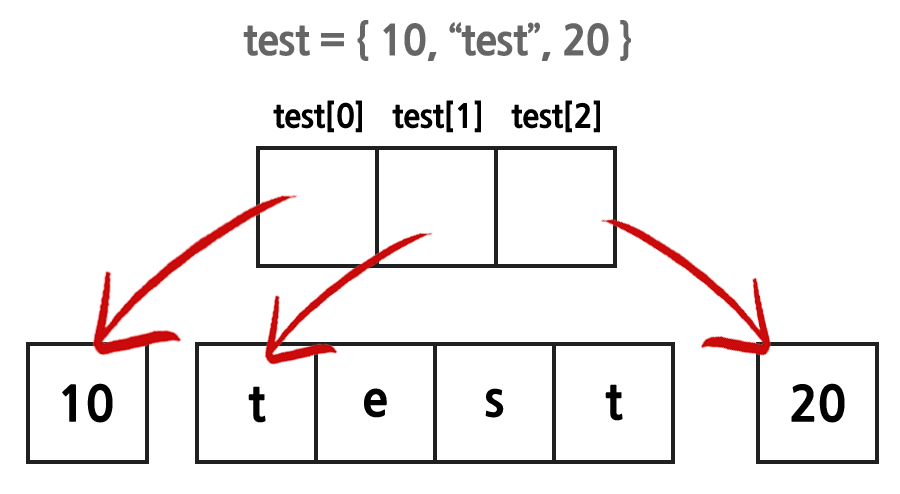
✔ 배열의 경우도 마찬가지로 데이터를 저장하는 것이 아니라 주소 값을 의미한다.
✔ 배열의 요소가 주소 값을 의미하기 때문에 배열에 서로 다른 형태의 데이터를 저장할 수 있다.
✔ 참고로 파이썬은 시스템 변수, file 등 모든 것들을 객체로 본다.
a = 10
a = 20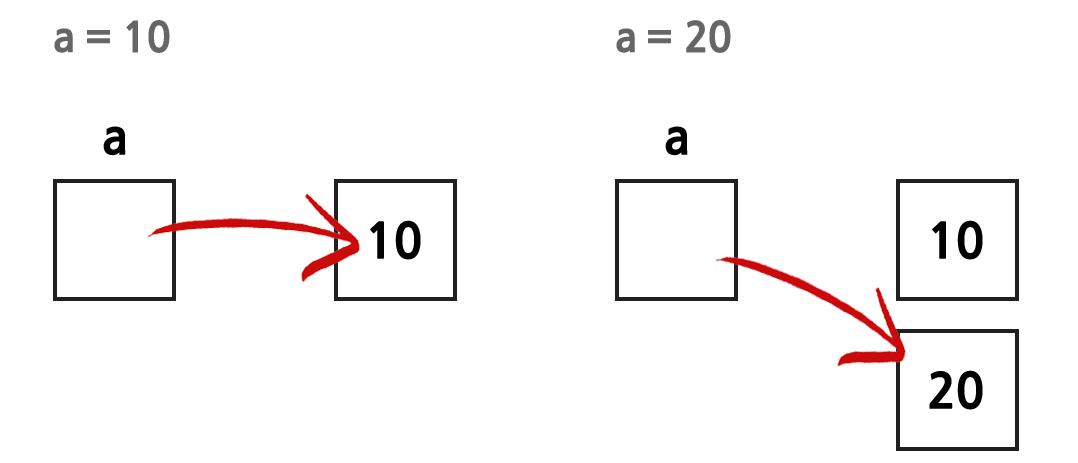
✔ a에 10을 할당했다가 20으로 재할당하면 a가 참조하는 주소 값이 바뀌었다고 볼 수 있다.
✔ 10은 더 이상 사용하지 않는 데이터이므로 시간이 지나면 가비지 컬렉터에 의해 자동 소멸된다.
✔ 사용자 입장에서는 필요 없는 데이터를 자동 정리해주니까 편리하지만, 이는 속도가 떨어지는 원인이 된다.
👉 산술 연산자
| 산술 연산자 | 설명 |
| + | 더하기 |
| - | 빼기 |
| * | 곱하기 |
| / | 나누기 |
| % | 나머지 연산 (정수만 가능) |
| // | 소수점 이하 절삭 (몫) |
| ** | 거듭 제곱 |
✔ 나누기 연산의 결과는 항상 실수
👉 할당 연산자
| 할당 연산자 | 예시 | 설명 |
| = | x = 2 | x에 2를 저장 |
| += | x += 2 | x = x + 2 와 동일한 표현 |
| -= | x -= 2 | x = x - 2 와 동일한 표현 |
| *= | x *= 2 | x = x * 2 와 동일한 표현 |
| /= | x /=2 | x = x / 2 와 동일한 표현 |
| %= | x %=2 | x = x % 2 와 동일한 표현 |
| **= | x **=2 | x = x + 2 와 동일한 표현 |
👉 연산자 우선순위
| 우선순위 | 연산자 | 의미 |
| 1 | ( ) [ ] { } | 괄호, 리스트, 딕셔너리, 세트 등 |
| 2 | ** | 지수 |
| 3 | + - ~ | 단항 연산자 |
| 4 | *, /, %, // | 산술 연산자 |
| 5 | + - | |
| 6 | << >> | 비트 시프트 연산자 |
| 7 | & | 비트 논리곱 |
| 8 | ^ | 비트 배타적 논리합 |
| 9 | | | 비트 논리합 |
| 10 | >, >=, <, <= | 관계 연산자 |
| 11 | ==, != | 동등 연산자 |
| 12 | =, %=, /=, //=, -=, +=, *=, **= | 대입 연산자 |
| 13 | not | 논리 연산자 |
| 14 | and | |
| 15 | or | |
| 16 | if ~ else | 조건문 |
[참고] 엘리스 트랙-혼자 공부하는 파이썬 / 길벗-파이썬 코딩 도장 / 엘리스 트랙 - 예제 중심의 파이썬 입문 / 위키백과
'BackEnd > Python' 카테고리의 다른 글
| [파이썬 기초] 01-4. 비트 연산자 / 논리 검증 (0) | 2021.03.16 |
|---|---|
| [파이썬 기초] 01-3. 문자열 / 문자열 메소드 / 입출력함수 (0) | 2021.03.16 |
| [파이썬 기초] 01-1. 파이썬의 특징과 기본 문법 (0) | 2021.03.15 |
| [파이썬 기초] 00-2. 파이썬 기초 속성 복습 (0) | 2021.03.09 |
| [파이썬 기초] 00-1. 파이썬 기초 속성 복습 (1) | 2021.03.07 |
