티스토리 뷰

1. malloc과 포인터 복습
int main(void){
int *x, *y;
x = (int*)malloc(sizeof(int));
*x=42; //동적할당받은 메모리에 저장
*y=13; //가리키는 메모리공간이 없으므로 error!
}✔ 포인터로 선언만 되었고, 어디를 가리킬지에 대해 정의되지 않았으므로 오류가 발생한다
2. 배열의 크기 조정하기
#include <stdio.h>
#include <stdlib.h>
int main(void){
int* listA = (int*)malloc(sizeof(int)*3);
if(listA == NULL) return 1;
listA[0] = 1;
listA[1] = 2;
listA[2] = 3;
//listA보다 큰 동적메모리 할당받기
int* listB = (int*)malloc(sizeof(int)*5);
for(int i=0; i<3; i++){
listB[i] = listA[i];
}
if(listB == NULL) return 1;
listB[3] = 4;
listB[4] = 5;
//더이상 사용하지 않는 동적 메모리 listA 해제
free(listA);
}
✔ listA보다 더 큰 크기의 배열인 listB를 선언하고, listA크기만큼 for문을 사용해 요소의 값을 하나하나 복사해 옮긴다.
✔ 이런 작업은 O(n), 즉 arrA의 크기 n 만큼의 실행시간이 소요된다.
✔ 위와 같은 과정을 함수 realloc()을 사용해 수행할 수도 있다.
#include <stdio.h>
#include <stdlib.h>
int main(void){
int* listA = (int*)malloc(sizeof(int)*3);
if(listA == NULL) return 1;
listA[0] = 1;
listA[1] = 2;
listA[2] = 3;
//listB 포인터에 메모리를 할당받기
int* listB = (int*)realloc(listA, sizeof(int)*5);
if(listB == NULL) return 1;
listB[3] = 4;
listB[4] = 5;
free(listA);
}
✔ 기존의 메모리 공간과 아예 다른 메모리 공간을 할당받던 첫 번째 방법과는 다르게
✔ realloc()은 크기 변경을 원하는 메모리를 가리키는 포인터 변수를 인수로 받는다.
✔ 인수로 받아온 포인터 변수를 통해 기존 메모리 공간의 크기를 바꾸어준다.
✔ 만약 해당 메모리와 연속된 공간으로 확장할 수 있다면 같은 메모리 주소를 반환하고
✔ 그렇지 않다면 새로운 메모리 주소를 반환한다.
3. 연결 리스트
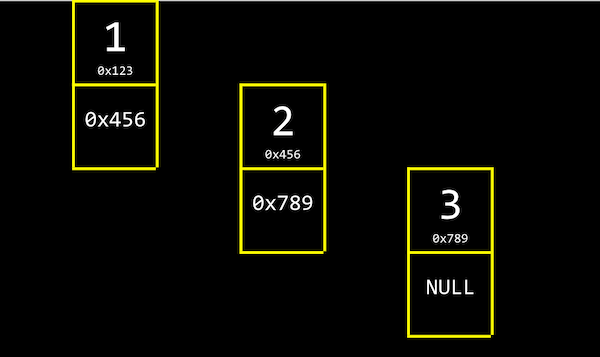
✔ 데이터 구조는 컴퓨터 메모리를 더 효율적으로 관리하기 위해 정의하는 구조체.
✔ 배열처럼 연속적인 메모리가 아니라, 다음 값의 메모리 주소를 기억하고 있어도 값을 이어서 읽어올 수 있다.
✔ 이런 형태를 연결 리스트라고 한다.
✔ 각 인덱스의 메모리 주소에서 자신의 값과 함께 바로 다음 값의 주소(포인터)를 저장한다.
✔ 연결 리스트는 간단한 구조체를 사용해 정의할 수 있다.
typedef struct node {
int num;
struct node *next;
} Node;✔ number는 자신이 가지는 값이고, 포인터 변수 next를 사용해 다음 요소의 주소를 가리킨다.
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
int num;
struct node * next;
}Node;
int main(void){
Node *n = NULL;
Node n1 = {1, NULL};
Node n2 = {2, NULL};
Node n3 = {3, NULL};
n1.next = &n2;
n2.next = &n3;
for( n=&n1; n!=NULL; n=n->next ){
printf("%d\n",n->num);
}
}
✔ 연결리스트의 시작인 n1의 주소를 저장할 구조체 변수 n을 선언
✔ for문을 사용해 n1의 주소로 초기화하고, n이 NULL일 때까지 반복한다.
✔ 증감식 대신, next에 저장된 주소로 값을 바꾸어준다.
✔ 연결리스트는 새로운 값을 추가할 때 다시 메모리를 할당하지 않아도 된다는 장점이 있다.
✔ 하지만 원하는 요소 바로 접근하기 힘들다. 하나하나 주소를 따라가야 한다는 점이 단점이다.
✔ 따라서 연결리스트의 크기가 n 일 때, 실행 시간은 O(n)이 된다.
4. 연결 리스트 : 트리
✔ 트리는 연결리스트를 기반으로 하는 새로운 데이터 구조.
✔ 연결리스트에서의 각 노드들의 연결이 1차원 적으로 구성되었다면, 트리에서는 2차원적으로 구성되었다고 볼 수 있다.
✔ 각 노드는 일정한 층에 속하고, 다음 층의 노드를 가리키는 포인터를 가진다.
✔ 트리의 최상층 노드를 루트라고 하며, 다음 층의 노드를 자식 노드라고 한다.

✔ 위 그림은 이진 검색 트리를 묘사한 이미지인데, 각 노드가 구성된 구조를 살펴보면 일정한 규칙을 찾을 수 있다.
✔ 하나의 노드는 두개의 자식 노드를 가지며, 왼쪽 노드는 자신의 값보다 작고, 오른쪽 노드는 자신의 값보다 크다.
✔ 즉, 이러한 트리 구조는 이진 검색을 수행하는 데에 유리하다.
typedef struct node {
int num;
struct node * left;
struct node * right;
}Node;
// 이진 검색 함수 (*tree는 이진 검색 트리를 가리키는 포인터)
bool search(node *tree) {
// 트리가 비어있는 경우 ‘false’를 반환하고 함수 종료
if (tree == NULL){
return false;
}
// 현재 노드의 값이 50보다 크면 왼쪽 노드 검색
else if (50 < tree->number) {
return search(tree->left);
}
// 현재 노드의 값이 50보다 작으면 오른쪽 노드 검색
else if (50 > tree->number) {
return search(tree->right);
}
// 위 모든 조건이 만족하지 않으면 노드의 값이 50이므로 ‘true’ 반환
else {
return true;
}
}
✔ 이진 검색 트리를 활용하면 검색 실행 시간과 노드 삽입 시간은 모두 O(log n)이다.
5. 해시 테이블

✔ 해시 테이블은 말하자면 연결 리스트의 배열.
✔ 해시 함수에 의해 어떤 요소에 저장될지가 결정되며, 요소는 또 다른 요소를 가리키며 연결 리스트가 된다.
✔ 해시 테이블의 검색 시간은 해시 함수에 따라 다르며, 이상적인 경우 검색시간은 O(1)이 된다.
✔ 각 요소에 모두 값이 저장되어 있다면 O(n)이 될 수 도 있다.
✔ 일반적으로는 최대한 많은 배열을 만드는 해시 함수를 사용하기 때문에 거의 O(1)에 가깝다고 볼 수 있다.
5. 트라이
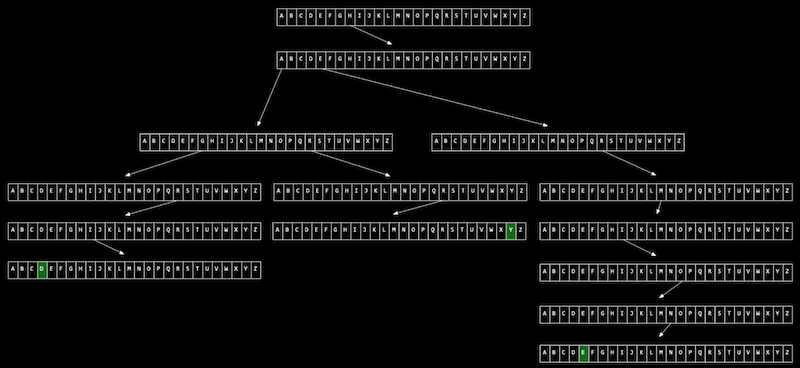
✔ 트라이는 기본적으로 트리 형태의 자료 구조이며 각 노드가 배열의 형태로 이루어져 있다는 특징을 가진다.
✔ 예를 들어 영어 알파벳으로 이루어진 문자열 값을 저장한다면, 이 노드는 a~z까지의 값을 가지는 배열이 된다.
✔ 그리고 알파벳은 다음 층의 노드 (a~z)를 가리킨다.
✔ 검색하는데 걸리는 시간은 문자열의 길이에 따라 다르다. 일반적인 영어 이름의 길이가 n이면 검색시간은 O(n)이다.
✔ 하지만 대부분의 이름은 그리 크지 않은 상수값이기 때문에 O(1)과 마찬가지라고 볼 수 있다.
✔ 검색 속도는 빠를 수 있지만, 메모리는 많이 차지하는 단점이 있다.
6. 스택 / 큐 / 딕셔너리
6-1. 큐
큐는 메모리 구조에서와 같이 값이 아래로 쌓이는 구조. 값을 넣고 뺄 때에는 선입 선출 또는 FIFO 방식을 따른다.
배열이나 연결 리스트를 통해 구현할 수 있다.
6-2. 스택
값이 위로 쌓이는 구조. 후입 선출 또는 LIFO 방식을 따른다. 말하자면 뷔페에서 쌓아둔 접시처럼 가장 위의 접시를 가장 먼저 들고 가는 것과 동일하다. 배열이나 연결리스트를 통해 구현할 수 있다.
6-3. 딕셔너리
딕셔너리는 key와 value로 이루어져 있다. key에 해당하는 value를 저장하고 읽어온다.
일반적인 의미로 보면 해시 테이블과 동일한 개념이라고 볼 수 있다. 딕셔너리에서는 key의 정의가 중요하다.
[출처] 부스트 코스 | 모두를 위한 컴퓨터 과학(CS50 2019)
'Computer Science > CS50' 카테고리의 다른 글
| [CS50 코칭스터디 2기] 끝났다🎉🎉 (0) | 2021.03.14 |
|---|---|
| [CS50 5주차] 8-9. 파일 쓰기/파일 읽기 (0) | 2021.02.14 |
| [CS50 5주차] 7. 메모리 교환, 스택, 힙 (0) | 2021.02.14 |
| [CS50 5주차] 6. 메모리 할당과 해제 (0) | 2021.02.12 |
| [CS50 5주차] 3-5. 문자열 (0) | 2021.02.12 |
